1. χ2 검정
1) 개념
- 종속변수와 독립변수가 명목 척도일 때 사용하는 검정 방법
2) 목적
- 1개 변수 : 변수 내 그룹 간의 비율이 같은지 다른지 알기 위해 평균을 비교
- 2개 변수 : 변수 사이의 연관성이 있는지 확인하는 목적
3) 공식
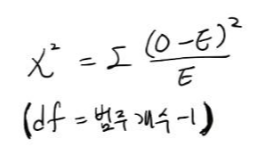
O : 관찰 빈도
E : 기대 빈도
4) 특징
- 범주의 종류가 많아질수록 χ2 그래프가 오른쪽으로 평탄해지는 경향이 있음

[출처] https://ko.wikipedia.org/wiki/%EC%B9%B4%EC%9D%B4%EC%A0%9C%EA%B3%B1_%EB%B6%84%ED%8F%AC
카이제곱 분포 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 카이제곱 분포(χ제곱分布, 영어: chi-squared distribution) 또는 χ2 분포는 k {\displaystyle k} 개의 서로 독립적인 표준정규 확률변수를 각각 제곱한 다음 합해서 얻어지
ko.wikipedia.org
2. 2변수 χ2 검정
EX) 휴대폰 사용과 뇌암 판정 간의 연관성 여부
1) 가설
H0 : brain cancer와 cell phone 사용에 연관성이 존재하지 않는다.(상호 독립)
Ha : brain cancer와 cell phone 사용에 연관성이 존재한다.
2) 계산
- 원래 데이터에서 셀별 기대 빈도를 산출
- 기대빈도 E=(i행의 총합 * i열의 총합) / 전체 데이터 합

- χ2 = Σ (관측값 - 기댓값)^2 / 기댓값
- 자유도는 cell phone 데이터 범주 2개, brain cancer 데이터 범주 2개로 (2-1)*(2-1) = 1

3. χ2 검정의 한계
1) 개수(count)로 집계한 데이터에 적용 가능
2) 각 셀의 기대 빈도가 5 이상이어야 함.
- 기대빈도가 낮을 경우 범주를 합치기도 한다.
- 범주를 합칠 수 없다면 피셔 정확도 검정이나 G-test(likelihood ratio test) 필요
(피셔 정확 검정은 다음 블로그 글 참고)
3) df=1인 경우
- χ2는
- 그런데 범주가 너무 작으면 연속성이 떨어지게 됨. 이 경우, 연속성을 보장하는 Yate's Correction 사용해야 한다.
'Data_Analysis > 기초통계' 카테고리의 다른 글
| [기초 통계] 선형 회귀 모델 (Linear Regression Model) (0) | 2020.11.15 |
|---|---|
| [기초통계] 공분산(Covariance) (0) | 2020.10.26 |
| [기초통계] 결정계수 R square, 상관 계수 R (0) | 2020.10.26 |
| 기초통계 - 이분산성(Heteroskedasticity) (0) | 2020.10.23 |
| 기초 통계 - Anova(three-way) (0) | 2020.10.23 |




댓글